ก็ขอแสดงความยินดีเป็นอย่างยิ่งที่ครบรอบก่อตั้งปีที่สองของบริษัทเคเอ็นเอสเอ็นจิเนียริ่งจำกัด ในฐานะผมที่เป็นคนสนิทชิดเชื้อกับทีมงานผู้ก่อตั้งก็ขอแสดงความยินดีนี้เป็นบทความในงานสำรวจ มาเที่ยวนี้ค่อนข้างหนักหน่อยจะพูดถึงเรื่องการคำนวณงานสำรวจด้วยวิธี Least Square ซึ่งแต่ละคนที่เรียนมาสายนี้จะรับรู้รับทราบว่าเป็นเรื่องหินเพียงใด แต่มาครั้งนี้มีตัวช่วยมาด้วยที่ทำให้งานคำนวณกลายเป็นเรื่องง่ายๆครับ
ในบางสถานการณ์ต้องขยายหมุดจากหมุดเดิมที่เป็นหมุดคู่ GNSS ไปอีกคู่หนึ่งไม่ไกลกันมากนักและใช้กล้อง Total Station โจทย์คือต้องการให้ค่าพิกัดหมุดคู่ใหม่ถูกต้องและแน่นหนาพอ เหตุผลเนื่องจากหมุดคู่ GNSS เดิมอยู่ใกล้แนวก่อสร้างอาจจะโดนรบกวน ในลักษณะนี้ต้องใช้การวัดแบบ Triangulation หรือโครงข่ายแบบสามเหลี่ยมมาช่วย แต่จะใช้โปรแกรมอะไรมาช่วย ผมรู้ว่ามีใน Civil3D และ Trimble Business Center แต่ไม่เคยใช้ ลองเมียงมองมายังขาเก่าในวงการสำรวจมานานแล้วคือ Microsurvey ที่มีโปรแกรมด้านสำรวจบน Desktop PC และ Mobile Handheld มาอย่างยาวนาน ผมทราบว่า Microsurvey มีโปรแกรมด้านนี้ชื่อ Microsurvey Star*net แต่จนแล้วจนรอดก็ไม่เคยได้ใช้สักที แต่เมื่อไม่นานนี้มีความจำเป็นบังคับต้องใช้งาน เอาละมาวันนี้ผมจะมารีวิว Microsurvey Star*Net พอหอมปากหอมคอเป็นแนวทางให้ผู้อ่านสามารถนำไปใช้ประยุกต์ได้ แต่ขอบอกว่า Microsurvey ใจป้ำพอสมควร ถ้ามีหมุดไม่เกิน 10 หมุด ข้อมูลรังวัดดิบๆ (observation) ไม่เกิน 100 ข้อมูล สามารถใช้งานได้ฟรี คำนวณจัดเต็มได้ทุกฟีเจอร์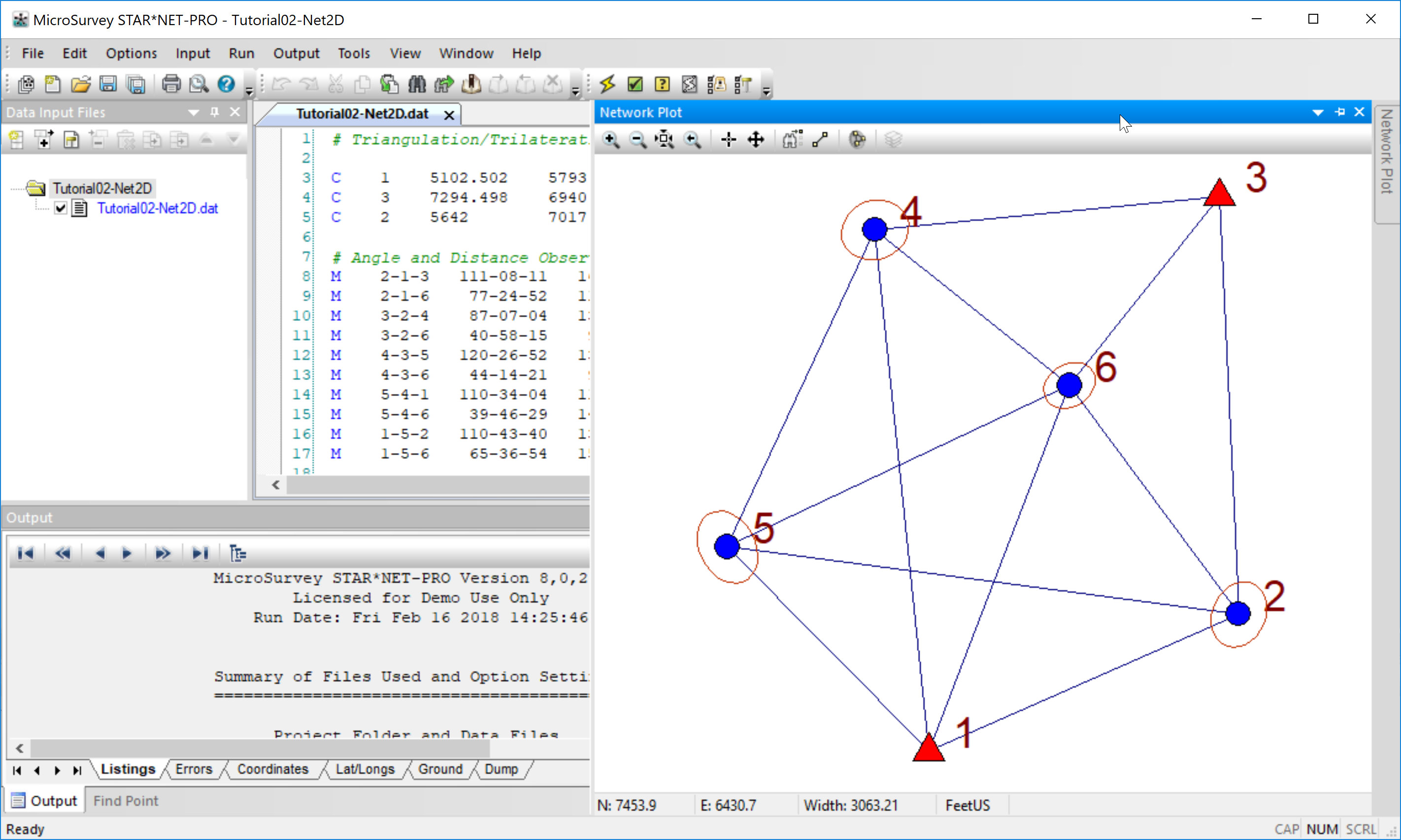 
เป็นที่รู้กันดีว่างานสำรวจที่ต้องเกี่ยวข้องกับการรังวัดหลายๅประเภทเช่นวัดระยะทาง วัดมุม วัดค่าระดับ จะไม่สามารถวัดให้ค่าออกมาเท่ากับค่าจริง และการวัดค่าทุกๆครั้งจะมีค่า error เช่น error ที่เกิดจากเครื่องมือและ error ที่เกิดจากคนอ่าน หรือไม่ error จากสภาพอากาศและสิ่งแวดล้อม ดังนั้นงานสำรวจจะมีการอ่านค่ามาหลายๆครั้ง ถ้าค่าใกล้เคียงกันแสดงว่ามี Precision (ความเที่ยงตรงหรือความแม่นยำ) สูง ตัวอย่างเช่นต้องการวัดมุมของวงรอบหนึ่งมุมด้วยกล้อง total station จำนวน 6 ชุด จะอ่านหน้าแล้วซ้ายหน้าขวาถ้าค่าต่างกันไม่เกิน 5" จะทำการเฉลี่ย จากนั้นเริ่มวัดใหม่จนสุดท้ายจะได้ค่ามุม 6 มุม แต่ละชุดถ้าค่าต่างกันไม่เกิน 10" ก็เป็นอันว่านำไปเฉลี่ยเพื่อใช้งานได้ หมายเหตุอีกนิดคำว่า Precision (ความแม่นยำ) กับ Accuracy (ความถูกต้อง) นั้นต่างกัน Precision ดีหมายถึงวัดแต่ละค่ามาใกล้เคียงกันมาก แต่เครื่องมือมี error แฝงอยู่ (เช่นเทปเหล็กวัดระยะมีการยืดตัว) ถ้าเราสามารถขจัด error นี้ออกไปได้จะกลายเป็นความถูกต้องสูงทันที
สังเกตว่าในการวัดมุมค่าต่างกันไม่เกิน 5" ในหน้าซ้ายและหน้าขวา และ 10" คือค่าต่างกันไม่เกินในแต่ละชุด ก็คือ Limit of Error เกณฑ์ความผิดพลาดที่เรายอมให้ได้ งานสำรวจทุกงานจะมีเกณฑ์ความผิดพลาดที่ยอมให้ได้ทุกงาน ยกตัวอย่างงานระดับจะถูกแบ่งงานระดับชั้นหนึ่ง งานระดับขั้นสอง ตลอดจนงานระดับขั้นสาม จะมีเกณฑ์ความผิดพลาดต่างกันและบางครั้งกำหนดระบุเครื่องมือเฉพาะด้วยเช่นงานระดับชั้นหนึ่ง ละเอียดที่สุดต้องใช้สตาฟที่เป็นสตาฟอินวาร์เท่านั้น เพราะสตาฟอินวาร์นั้นทำด้วยวัสดุที่รับรองได้ว่ามีการยืดหดตัวน้อยมาก
ความจริงการคำนวณด้วยวิธี Least square ผมจำได้แต่หลักการแต่ความรู้รายละเอียดคืนอาจารย์ที่เคารพไปหมดแล้ว แต่อย่างไรก็ตามมาดูกันสักนิด การคำนวณ Least Squares นำมาช่วนในกรณีที่มีการรังวัดเกิน (Redundant) มาจากจำนวนตัวแปรที่ไม่ทราบค่า ลองมาไล่กันไปดูทีละขั้นง่ายๆ โจทย์ขั้นที่ 1 หาค่าพิกัดจุด C วงกลมสีฟ้า ทราบค่าพิกัดจุดที่ 1 คือ N1, E1 และวัดค่ามุมได้ค่า A1 และวัดระยะทางได้ค่า D1 ตอนนี้ที่ทราบค่า 4 จำนวนคือค่าพิกัด N1, E1 และ A1 และ D1 และตัวที่ไม่ทราบค่าคือค่าพิกัดจุดวงกลมสีฟ้า (N = ?, E = ?) ไม่ทราบค่า 2 ตัวแปร เราสามารถหาค่าพิกัด N, E จุด C จุดวงกลมสีฟ้าได้จากสมการดังนี้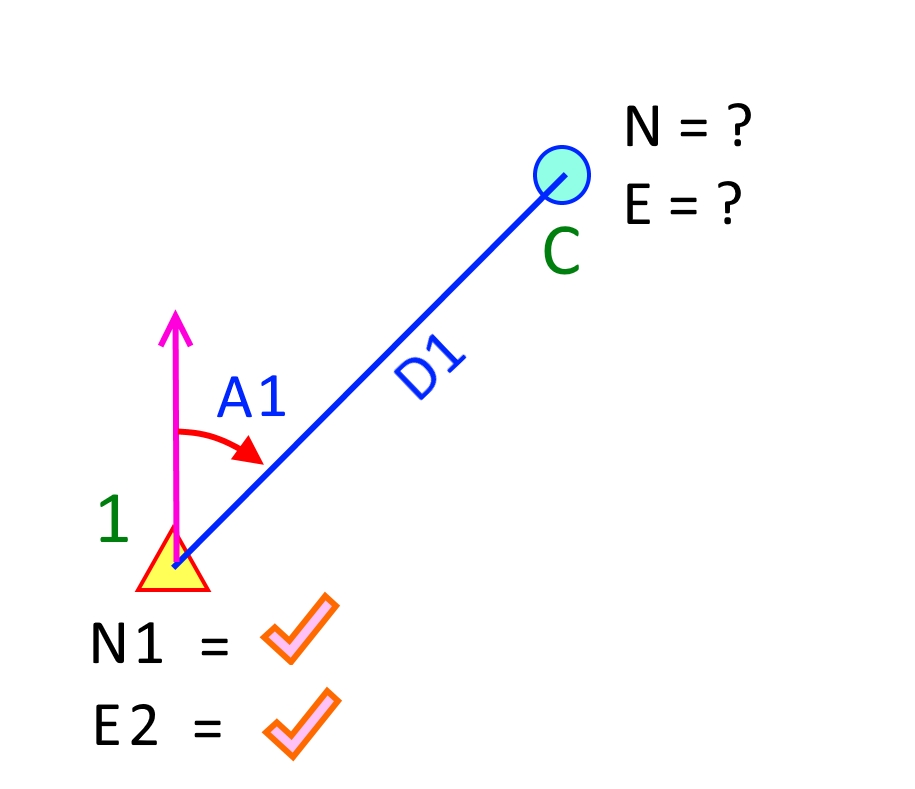 
N = N1 + D1 x Cos (A1) E = E1 + D1 x Sin(A1) จะเห็นว่าไม่ต้องใช้ Least Squares มาคำนวณเพราะค่าที่วัดมาคือ A1, D1 สามารถคำนวณหาค่าพิัดจุดวงกลมสีฟ้าได้เลยทันที แต่ปัญหาคือความน่าเชื่อถือค่าพิกัดของวงกลมสีฟ้าจะมีมากน้อยเพียงใดขึ้นอยู่กับมุม A1 และระยะทาง D1 ที่ต้องอาศัยการวัดซ้ำๆหลายครั้งแล้วใช้ค่าเฉลี่ย โจทย์ขั้นที่ 2 ทราบค่าพิกัดจุดที่ 1 และจุดที่ 2 ต้องการหาค่าพิกัด N,E จุด C วงกลมสีฟ้า แต่วัดมุม A2 และระยะทาง D2 มาเพิ่มจากจุดที่ 2 คำนวณค่าพิกัดจุด C จากจุดที่ 1 จะได้ค่า N, E มา N = N1 + D1 x Cos (A1) E = E1 + D1 x Sin(A1) ครั้งที่ 2 คำนวณจากจุดที่ 2 N = N2 + D2 x Cos (A2) E = E2 + D2 x Sin(A2) จะได้ค่าพิกัดจุด C มาสองค่า ถ้าค่าพิกัด N, E ใกล้เคียงกันมาก แสดงว่าการวัดมุม A1, A2 และระยะทาง D1, D2 ละเอียดคือ precision ดี แต่ปัญหาที่เกิดขึ้นจะทำอย่างไรกับค่าพิกัด N, E สองค่านี้ โจทย์นี้สามารถใช้ Least Square มาช่วยคำนวณได้ในกรณีรังวัดมาเกิน (Redundant) โจทย์ขั้นที่ 3 วัดมุม A3 และระยะทาง D3 มาเพิ่มจากจุดที่ 3 ที่นี่การคำนวณจะได้ค่าพิกัดจุด C ทั้งหมดสามค่า การคำนวณหาค่าพิกัดจุด C ใช้ Least Square จะได้ค่าออกมาดีที่สุด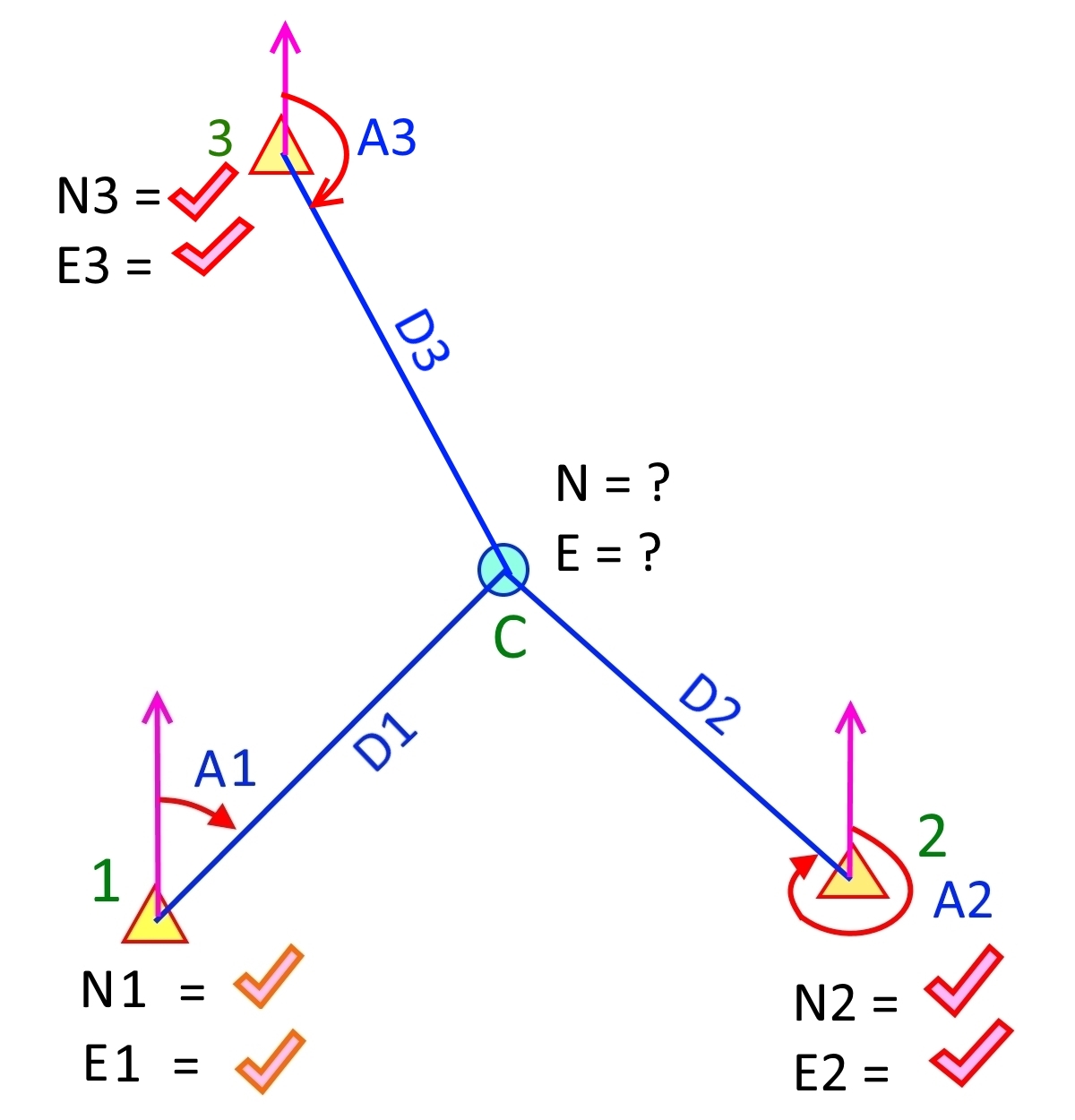 
จากตัวอย่างด้านบนยังเป็นลักษณะง่ายๆ แต่ถ้าเป็นโครงข่ายวงรอบแบบเน็ตเวิร์ค จะซับซ้อนขึ้นมามาก การคำนวณด้วยวิธีแมนวลแบบสมัยก่อนนับว่าเป็นงานยากมหาหินทีเดียว งานคำนวณด้วย Microsurvey Star*Net ดูเหมือนยากแต่จริงๆแล้วค่อนข้างง่าย เพียงแต่ต้องเข้าใจรูปแบบการป้อนข้อมูลที่โปรแกรมต้องการ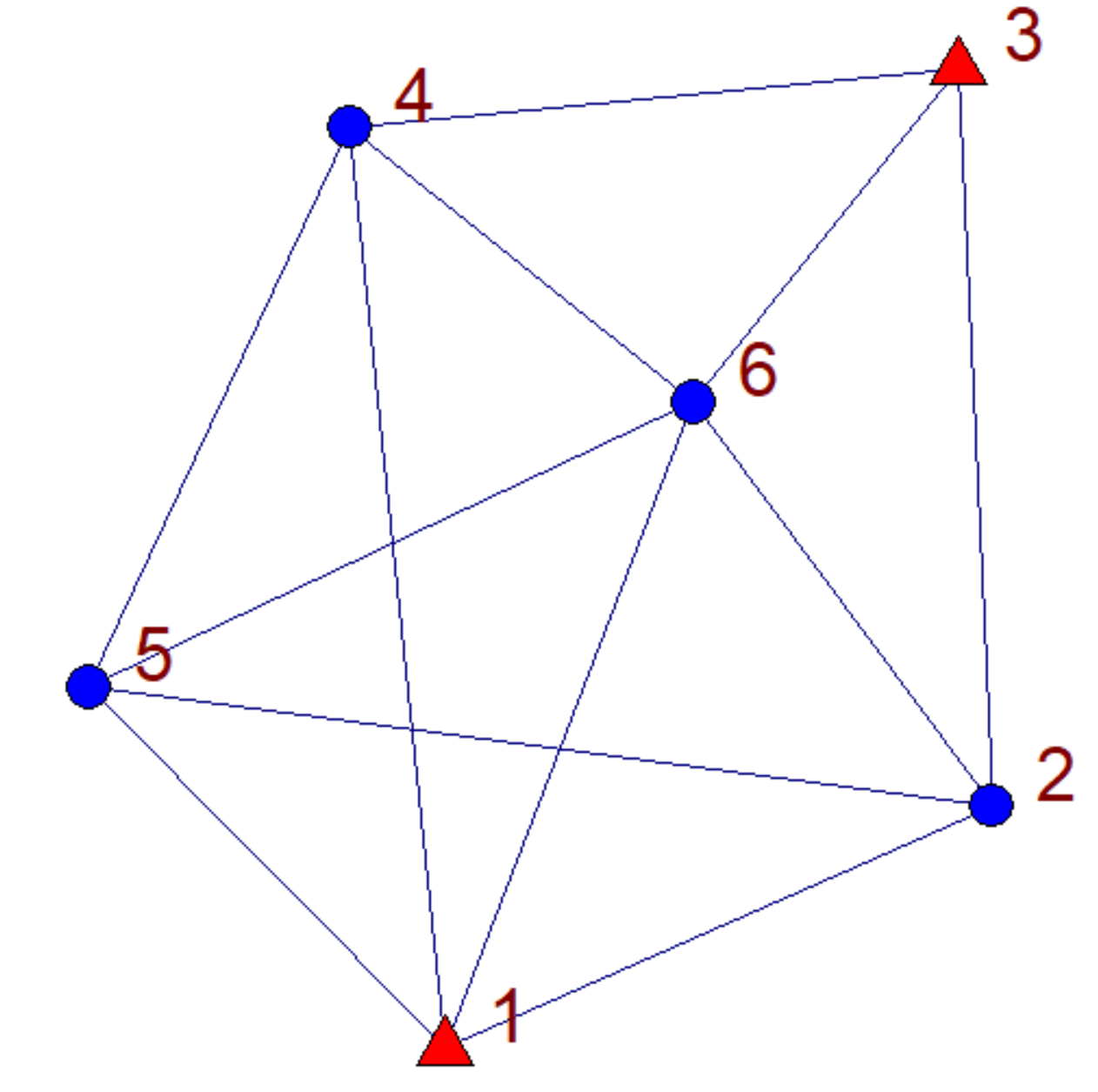 
มาดูในกรณีตัวอย่างของผม ผมมีหมุด GNSS คือ PBM2A/PBM2B ต้องการขยายหมุดไปยัง PBM2C/PBM2D เพราะว่าหมุด GNSS เดิมอยู่ใกล้บริเวณก่อสร้างมากเกินไป เกรงจะเกิดผลกระทบกระเทือนในอนาคต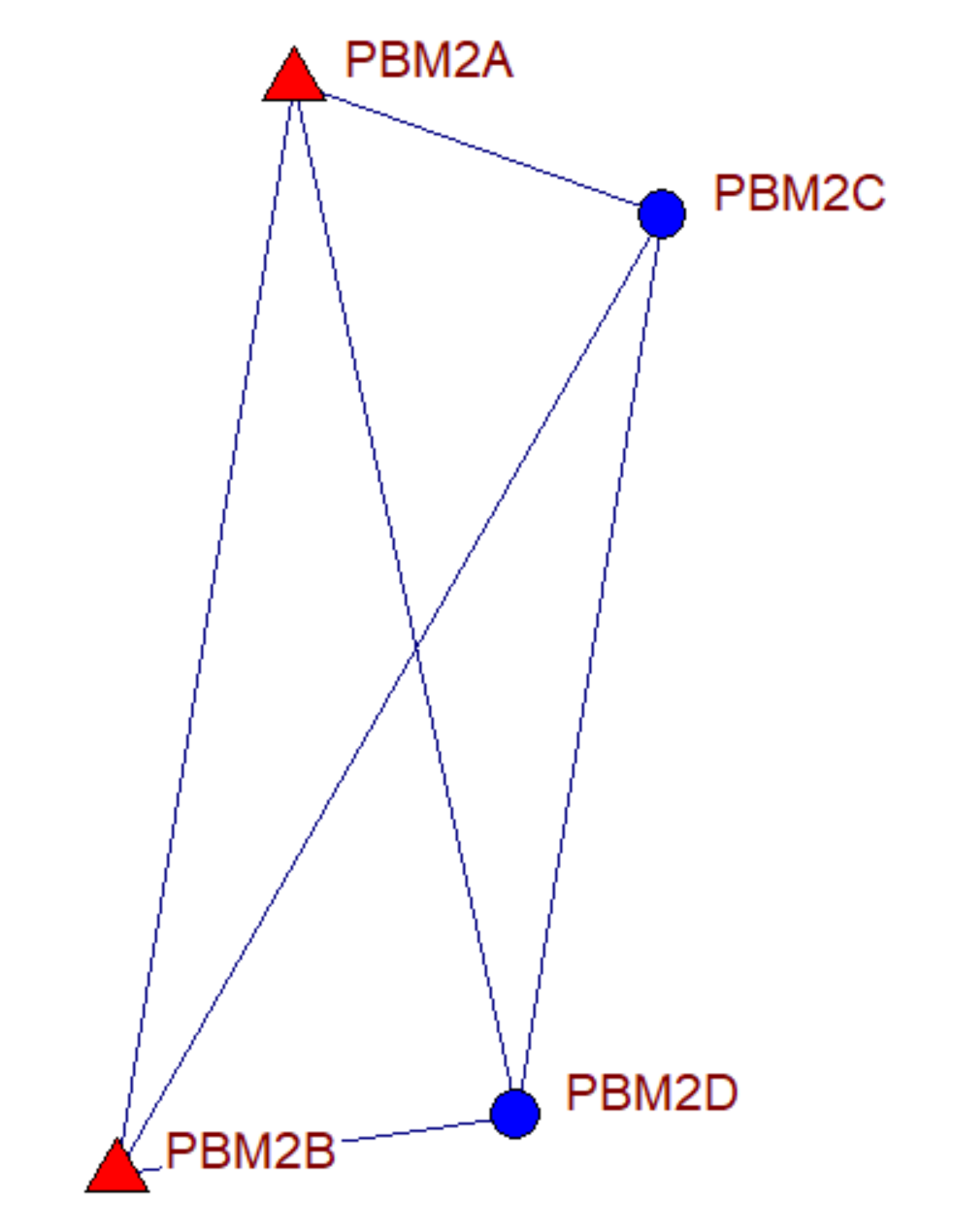 
ผมให้ทีมงานวัดมุมทุกง่ามมุมภายใน (มุมตามเข็มนาฬิกา) และวัดระยะราบดังรูปด้านล่าง จำนวนหมุดทั้ง 4 หมุด มีหมุดที่ทราบค่าพิกัด N, E จำนวน 2 หมุดและมีหมุดที่ไม่ทราบค่าพิกัด N, E อีกจำนวน 2 หมุด เนื่องจากจำนวนหมุดไม่เกิน 10 หมุดและข้อมูลดิบรังวัดไม่เกิน 100 ข้อมูล ดังนั้นผมสามารถใช้โปรแกรม Microsurvey Star*Net ได้ฟรีแบบเต็มฟีเจอร์ พื้นที่ที่ผมทำงานคำนวณ Combined Scale Factor (CSF) ได้เท่ากับ 1.00048005912 แต่ในการวัดระยะทางหน้างาน ผมให้ทีมงานใช้ 1.0 เพราะต้องการเอาทอนเข้าระนาบยูทีเอ็มด้วยโปรแกรม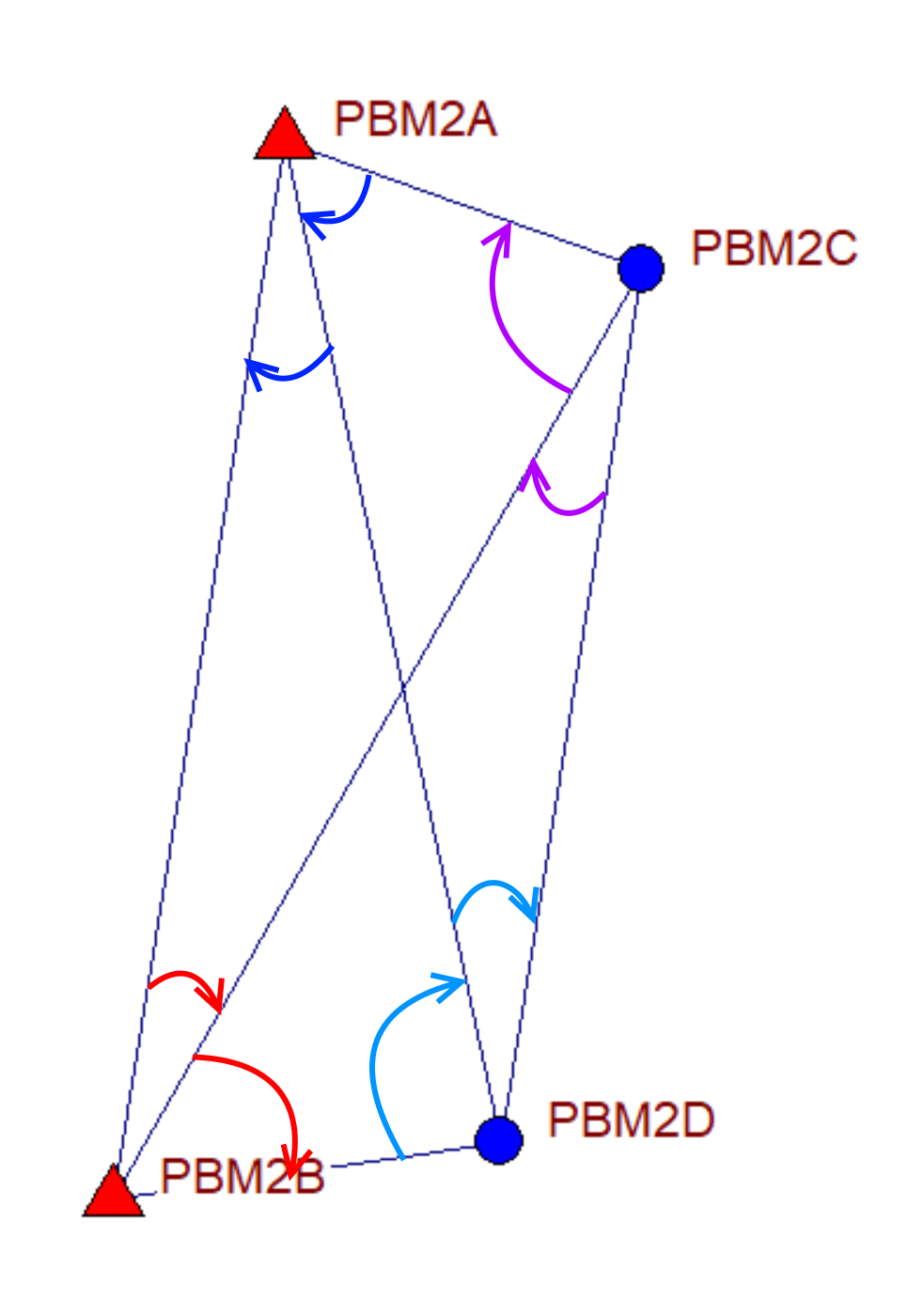 
เมื่อเปิดโปรแกรมมาแล้วต้องการสร้าง project ใหม่ใช้เมนู File => New Project... จากนั้นไดอะล็อกจะถามไฟล์ที่ต้องการจัดเก็บ เลือกโฟลเดอร์และป้อนชื่อที่ต้องการ เสร็จจากขั้นตอนนี้ต่อไปจะตั้งค่า options ก่อนได้แก่หน่วยระยะทาง มุม และค่า CSF เนื่องจากโครงการนี้ไม่ได้คิดค่าระดับดังนั้นผมเลือก Adjustment type เป็น 2D ส่วนหน่วยเลือกเป็น Meters (เมตร) มุมเลือกแบบ DMS (Degree-Minute-Second) หรือแบบองศาลิปดาและฟิลิปดา ส่วน Coordinate System ผมเลือกเป็น Local เพราะจะได้ใส่ CSF (ไม่ให้โปรแกรมคำนวณให้) คือค่า 1.00048005912 ที่ผมกล่าวไปแล้ว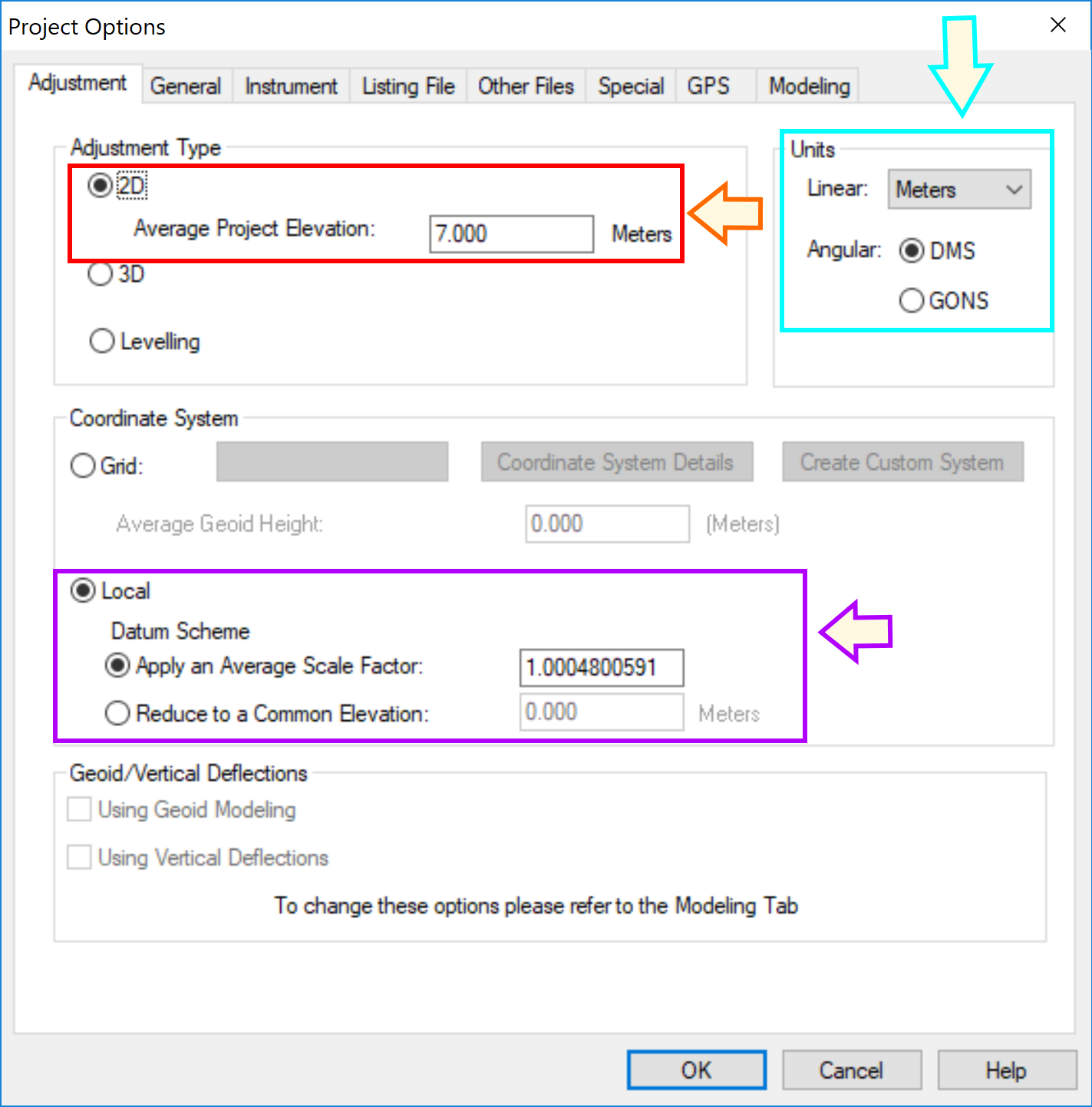 
สไตล์การป้อนข้อมูลของ Microsurvey Star*Net คล้ายๆ text file ต้องพิมพ์ลงไปสดๆ แต่ไม่ยาก มาดูข้อมูลของผม สามารถ copy ข้อมูลด้านล่างนี้ไปวางใน Microsurvey Star*Net ได้ครับ
# MicroSurvey STAR*NET V8 #.DATA OFF .2D .ORDER NE .ORDER AtFromTo C PBM2A 2640828.299 231601.340 ! ! ′CONTROL C PBM2B 2640605.876 231565.132 ! ! ′CONTROL M PBM2A-PBM2C-PBM2D 57-56-44 215.151 M PBM2A-PBM2D-PBM2B 21-20-27 225.244 M PBM2B-PBM2A-PBM2C 20-22-03 224.489 M PBM2B-PBM2C-PBM2D 52-01-36 82.133 M PBM2C-PBM2D-PBM2B 20-24-52 224.490 M PBM2C-PBM2B-PBM2A 80-21-02 79.522 M PBM2D-PBM2B-PBM2A 86-16-11 215.151 M PBM2D-PBM2A-PBM2C 21-17-11 185.614 D PBM2B-PBM2A 225.243 D PBM2D-PBM2B 82.132 D PBM2C-PBM2D 185.613 D PBM2A-PBM2C 79.521 #.DATA ON
เครื่องหมาย # นำหน้าเป็นคอมเมนต์จะไม่มีประมวลผลในบรรทัดนั้น .2D ตั้งว่าโครงการนี้จะคำนวณในแนวสองมิติ (2D) คือค่าพิกัดเท่านั้น มีผล Reset ค่าที่เราตั้งใน options .ORDER NE บอกลำดับว่าต้องการค่า Northing มาก่อน Easting .ORDER AtFromTo บอกลำดับของจุดตั้งกล้องและเป้าหน้าเป้าหลัง ผมเลือกใช้ AtFromTo ความหมายคือ จุดตั้งกล้อง - เป้าหลัง - เป้าหน้า ถ้า PBM2D-PBM2A-PBM2C หมายถึงตั้งกล้องที่หมุด PBM2D ส่องไปเป้าหลัง PBM2A และส่องไปเป้าหน้าคือ PBM2C แต่ถ้ารูปแบบนี้มันฝืนความรู้สึกก็สามารถเลือก FromAtTo ได้ครับ .SCALE 1.00048005912 คือค่า Combined Scale Factor ถ้าป้อนที่นี่จะรีเซ็ตค่าที่ตั้งไว้ใน options C คือ Control หมุดควบคุมตามด้วยชื่อ ค่าพิกัด N, E ถ้ารูปแบบ 2D N, E ใช้รูปแบบ
C Station North East [Std Errors] [′Description]
A คือวัดมุม (Horizontal Angle) มีรูปแบบคือ
A At-From-To Angle [Std Error] [′Description]
M คือรังวัดไปหาสถานีอื่น (All Measure to another station) แล้วใส่ชื่อจุดตั้งกล้องโดยเรียงลำดับตามที่เราตั้งไว้ใน .ORDER สำหรับผมแล้วเลือกใช้ AtFromTo จากนั้นต่อด้วยมุมและระยะทาง ใช้รูปแบบ 2D
M At-From-To Angle Distance [Std Errs] [′Description]
D คือระยะราบ (Distance)
D From-To Horizontal Distance [Std Error] [′Description]
เมื่อข้อมูลพร้อม ผมทำการคำนวณด้วยเมนู Run => Adjust Network! การคำนวณใช้เวลาแค่เสี้ยววินาทีจะได้ผลการคำนวณสรุปมาก่อนเป็น Processing summary แสดงผลเป็นบนไดอะล็อกดังรูป ซึ่งจะมีการคำนวณวนลูปอยู่สองครั้ง (2 iterations)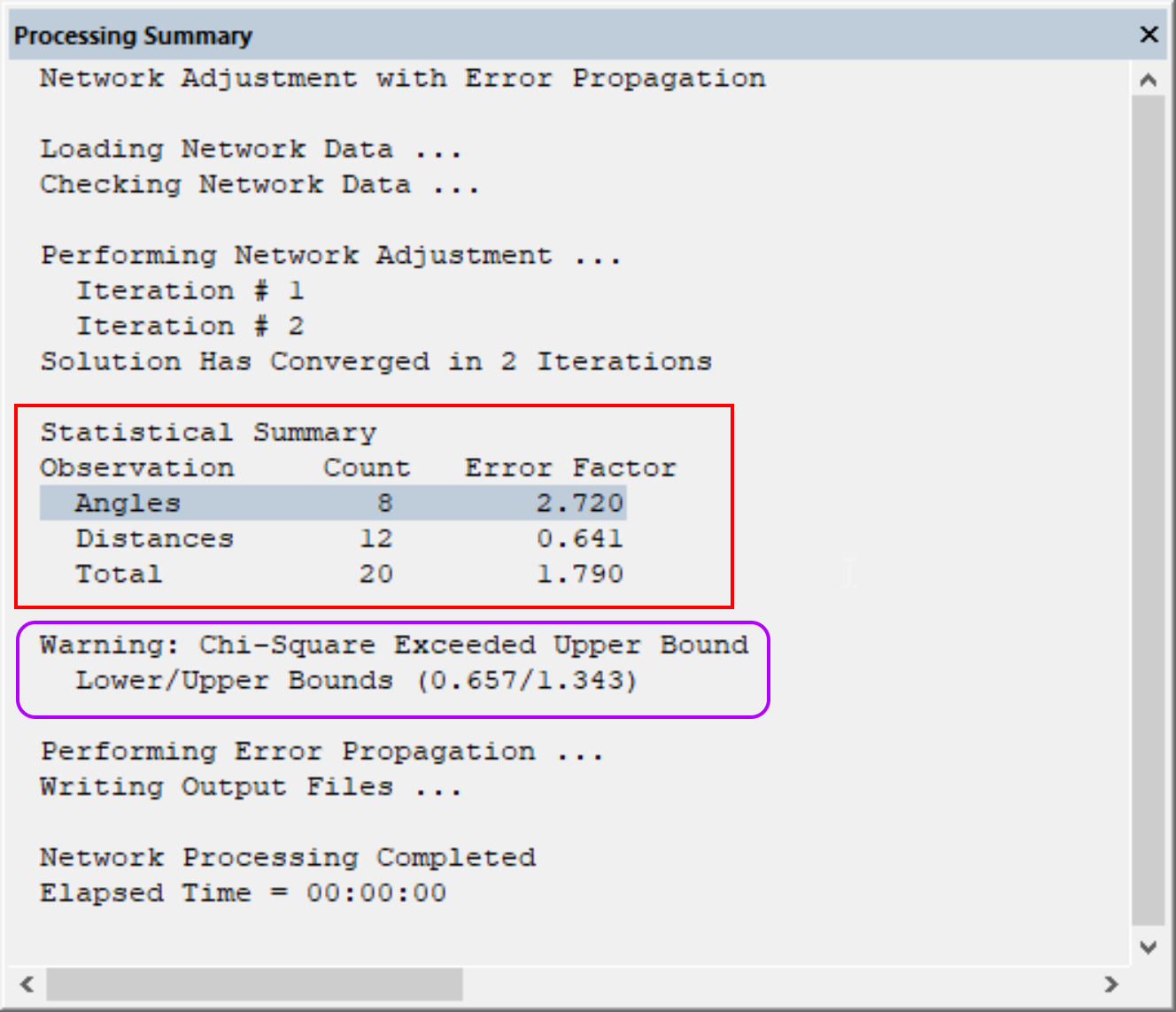 
กรอบแรกที่วงด้วยสีแดงสรุปจำนวนข้อมูลที่รังวัดมา จำนวนมุมทั้งหมด 8 มุม ระยะราบทั้งหมด 12 ระยะทาง รวมทั้งหมด 20 ข้อมูล ส่วน Error Factor คือสัดส่วนความผิดพลาด ดูแล้วความผิดพลาดทางมุมจะมากกว่าระยะทางอยู่มากทีเดียว ซึ่งความจริงก็เป็นเช่นนั้นเพราะว่าระยะทางที่วัดด้วยกล้อง Total Station เป็นที่รู้กันว่ามีความละเอียดสูง ส่วนการวัดมุมนั้นอาศัยทักษะของผู้อ่านกล้องช่างสำรวจอยู่มาก ในกรอบที่สองจะสรุปผลด้านสถิติ Chi-square ในลักษณะเตือนว่าข้อมูลเกินขอบเขตด้านบนด้านล่าง ก็แสดงว่าข้อมูลทีรังวัดมาไม่ดีนัก ส่วนผลการคำนวณแบบละเอียด ดูได้ที่แถบด้านล่าง "Listings" ของ Star*Net 
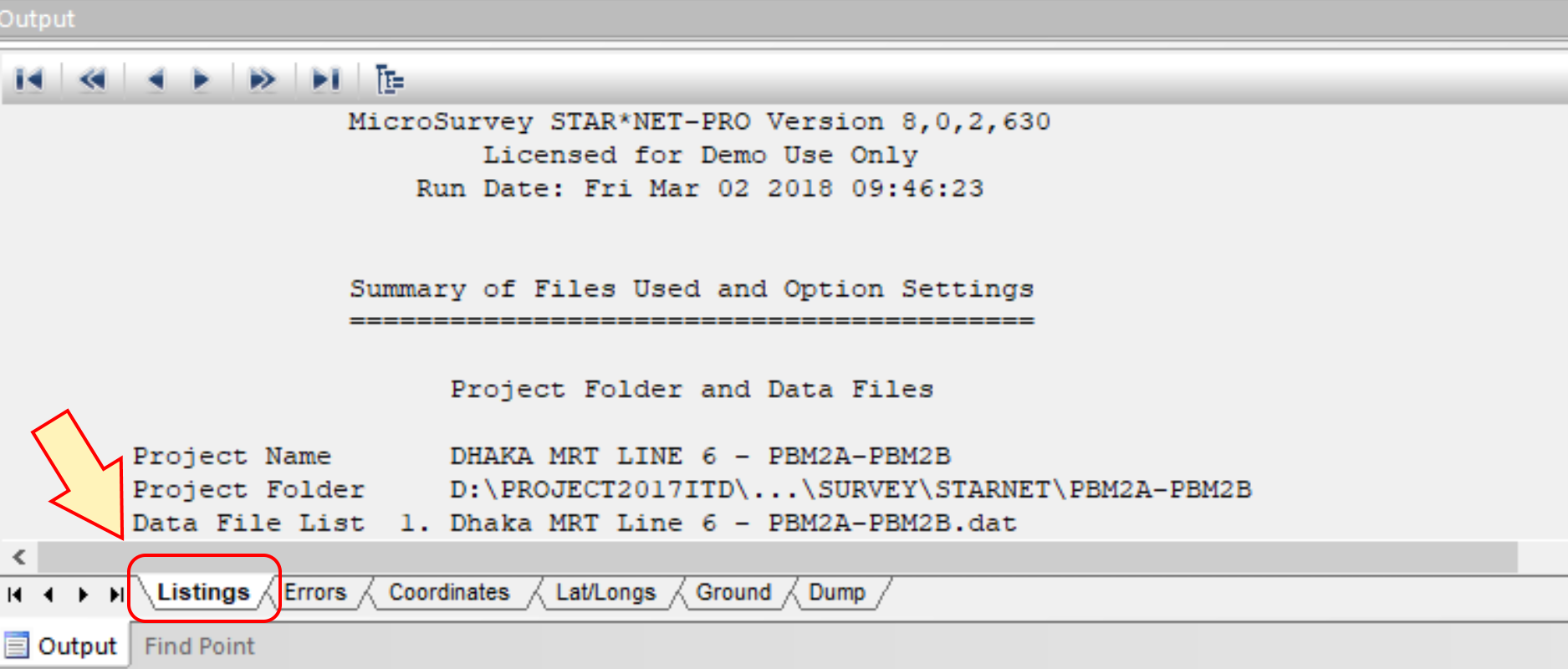
ผมคัดลอกมาให้ดูชัดๆดังกรอบด้านล่าง เปิดฉากมาด้วยการทวนรายการตั้งค่าไว้ใน Project Options ตามมาด้วย standard error ของเครื่องมือเรา ตัวนี้ผมปล่อยเป็นค่าปริยาย และก็มาถึงหมุดคอนโทรลที่ผมตั้งไว้ 2 หมุด (Number of Entered Stations (Meters) = 2) คือ PBM2A และ PBM2B
MicroSurvey STAR*NET-PRO Version 8,0,2,630 Licensed for Demo Use Only Run Date: Fri Feb 16 2018 18:38:14 Summary of Files Used and Option Settings ========================================= Project Folder and Data Files Project Name DHAKA MRT LINE 6 - PBM2A-PBM2B Project Folder D:PROJECT2017ITD...SURVEYSTARNETPBM2A-PBM2B Data File List 1. Dhaka MRT Line 6 - PBM2A-PBM2B.dat Project Option Settings STAR*NET Run Mode : Adjust with Error Propagation Type of Adjustment : 2D Project Units : Meters; DMS Coordinate System : LOCAL Default Project Elevation : 7.0000 Meters Apply Average Scale Factor : 1.00048005912 Input/Output Coordinate Order : North-East Angle Data Station Order : At-From-To Distance/Vertical Data Type : Slope/Zenith Convergence Limit; Max Iterations : 0.010000; 10 Default Coefficient of Refraction : 0.070000 Earth Radius : 6372000.00 Meters Create Coordinate File : Yes Create Ground Scale Coordinate File : No Create Dump File : No Instrument Standard Error Settings Project Default Instrument Distances (Constant) : 0.009144 Meters Distances (PPM) : 0.000000 Angles : 2.000000 Seconds Directions : 1.500000 Seconds Azimuths & Bearings : 2.000000 Seconds Centering Error Instrument : 0.000000 Meters Centering Error Target : 0.000000 Meters Summary of Unadjusted Input Observations ======================================== Number of Entered Stations (Meters) = 2 Fixed Stations N E Description PBM2A 2640828.2990 231601.3400 CONTROL PBM2B 2640605.8760 231565.1320 CONTROL
จากนั้นจะแสดงว่าพบมุมราบที่วัดมาทั้งหมด 8 มุม (Number of Angle Observations (DMS) = 8) พร้อมทั้งแสดงข้อมูลรังวัดมาทั้งหมด และไม่ลืมค่า Standard error ที่มาใช้ในการคำนวณคือ 2" ตามมาติดๆด้วยข้อมูลรังวัดระยะทางทั้งหมด 12 ข้อมูลซึ่ง Standard error ที่ใช้คือ 0.0091 และที่สำคัญคือค่า Combined Scale Factor (CSF) ที่ผมกำหนดไว้แล้วคือ 1.00048005912 แต่โปรแกรมแสดงผล 1.0004801 (ทศนิยมเจ็ดตำแหน่งเพียงพอ)
KNS-ENGINEERING
Number of Angle Observations (DMS) = 8
At From To Angle StdErr
PBM2A PBM2C PBM2D 57-56-44.00 2.00
PBM2A PBM2D PBM2B 21-20-27.00 2.00
PBM2B PBM2A PBM2C 20-22-03.00 2.00
PBM2B PBM2C PBM2D 52-01-36.00 2.00
PBM2C PBM2D PBM2B 20-24-52.00 2.00
PBM2C PBM2B PBM2A 80-21-02.00 2.00
PBM2D PBM2B PBM2A 86-16-11.00 2.00
PBM2D PBM2A PBM2C 21-17-11.00 2.00
Number of Distance Observations (Meters) = 12
From To Distance StdErr Scale
PBM2A PBM2D 215.1510 0.0091 1.0004801
PBM2A PBM2B 225.2440 0.0091 1.0004801
PBM2B PBM2C 224.4890 0.0091 1.0004801
PBM2B PBM2D 82.1330 0.0091 1.0004801
PBM2C PBM2B 224.4900 0.0091 1.0004801
PBM2C PBM2A 79.5220 0.0091 1.0004801
PBM2D PBM2A 215.1510 0.0091 1.0004801
PBM2D PBM2C 185.6140 0.0091 1.0004801
PBM2B PBM2A 225.2430 0.0091 1.0004801
PBM2D PBM2B 82.1320 0.0091 1.0004801
PBM2C PBM2D 185.6130 0.0091 1.0004801
PBM2A PBM2C 79.5210 0.0091 1.0004801
ต่อไปสรุปการคำนวณของ Least Square จำนวนหมุดทั้งหมด 4 หมุด เป็นหมุดคอนโทรล 2 หมุด ต้องการทราบค่าพิกัด 2 หมุด ซึ่งค่าพิกัดประกอบไปด้วย N,E แสดงว่าจำนวนที่ต้องการทราบค่าทั้งหมด 4 ค่า (Number of Unknowns - N,E ของ PBM2C และ N,E ของ PBM2D) ข้อมูลรังวัดมาทั้งหมด 20 ข้อมูล (Number of Observations) ลบด้วย Number of Unknows 4 ค่าจะได้ Number of Redundant Obs = 16 คือข้อมุลรังวัดเกินมานั่นเอง ซึ่งการรังวัดที่ข้อมูลที่เกินมานี้สามารถนำมาคำนวณ Least square ได้ตามที่กล่าวไปแล้วข้างต้น
Adjustment Statistical Summary
==============================
Iterations = 2
Number of Stations = 4
Number of Observations = 20
Number of Unknowns = 4
Number of Redundant Obs = 16
Observation Count Sum Squares Error
of StdRes Factor
Angles 8 47.339 2.720
Distances 12 3.946 0.641
Total 20 51.285 1.790
Warning: The Chi-Square Test at 5.00% Level Exceeded Upper Bound
Lower/Upper Bounds (0.657/1.343)
ต่อไปโปรแกรมแสดงสิ่งที่ผมต้องการคือค่าพิกัด N,E ของหมุด PBM2C และ PBM2D รายการต่อไปคือแสดง residual คือความแตกต่างระหว่างข้อมูลรังวัดที่มากับค่าที่คำนวณได้ ยิ่งน้อยยิ่งดีครับ ยิ่งใกล้ศูนย์ยิ่งต้องการ จะเห็นข้อมูลรังวัดมุมมีดาวติดไว้หลายตัว แสดงว่าข้อมูลรังวัดของมุมนั้นไม่ดีนัก ส่วนระยะทางนั้นดีอยู่แล้วจากเครื่องมือวัดระยะทางในปัจจุบัน ข้อมูลที่ผมนำมาทดสอบในครั้งนี้เพื่อเป็นกรณีศึกษา ในชีวิตจริงเมื่อคำนวณแล้วค่าออกมาไม่ดี ผมได้ให้ทีมงานไปรังวัดข้อมูลมาใหม่
Adjusted Coordinates (Meters)
=============================
Station N E Description
PBM2A 2640828.2990 231601.3400 CONTROL
PBM2B 2640605.8760 231565.1320 CONTROL
PBM2D 2640617.8267 231646.4337
PBM2C 2640801.1415 231676.1096
Adjusted Observations and Residuals
===================================
Adjusted Angle Observations (DMS)
At From To Angle Residual StdErr StdRes File:Line
PBM2A PBM2C PBM2D 57-56-43.31 -0-00-00.69 2.00 0.3 1:10
PBM2A PBM2D PBM2B 21-20-19.76 -0-00-07.24 2.00 3.6* 1:11
PBM2B PBM2A PBM2C 20-21-55.37 -0-00-07.63 2.00 3.8* 1:12
PBM2B PBM2C PBM2D 52-01-35.22 -0-00-00.78 2.00 0.4 1:13
PBM2C PBM2D PBM2B 20-24-57.06 0-00-05.06 2.00 2.5 1:14
PBM2C PBM2B PBM2A 80-21-01.56 -0-00-00.44 2.00 0.2 1:15
PBM2D PBM2B PBM2A 86-16-09.64 -0-00-01.36 2.00 0.7 1:16
PBM2D PBM2A PBM2C 21-17-18.08 0-00-07.08 2.00 3.5* 1:17
Adjusted Distance Observations (Meters)
From To Distance Residual StdErr StdRes File:Line
PBM2A PBM2D 215.1455 -0.0055 0.0091 0.6 1:10
PBM2A PBM2B 225.2427 -0.0013 0.0091 0.1 1:11
PBM2B PBM2C 224.4911 0.0021 0.0091 0.2 1:12
PBM2B PBM2D 82.1359 0.0029 0.0091 0.3 1:13
PBM2C PBM2B 224.4911 0.0011 0.0091 0.1 1:14
PBM2C PBM2A 79.5107 -0.0113 0.0091 1.2 1:15
PBM2D PBM2A 215.1455 -0.0055 0.0091 0.6 1:16
PBM2D PBM2C 185.6122 -0.0018 0.0091 0.2 1:17
PBM2B PBM2A 225.2427 -0.0003 0.0091 0.0 1:18
PBM2D PBM2B 82.1359 0.0039 0.0091 0.4 1:19
PBM2C PBM2D 185.6122 -0.0008 0.0091 0.1 1:20
PBM2A PBM2C 79.5107 -0.0103 0.0091 1.1 1:21
หนึ่งพันคำพูดไม่เท่ากับดูด้วยตาหนึ่งครั้ง เมื่อคำนวณแล้วสิ่งที่ผู้ใช้ต้องการมากที่สุดนอกจากรายการคำนวณที่ผานเกณฑ์คือรูปร่างของโครงข่าย นอกจากนั้นยังมีแสดงการกระจายของรูปร่างของวงรีที่แทน error ถ้าวงเล็กก็ดี ถ้าวงใหญ่แสดงว่า error มาก ก่อนอื่นตั้งค่า options ก่อน ผมเลือกที่ Show Ellipse, Show Rel Ellipse ดังไดอะล็อกบ็อก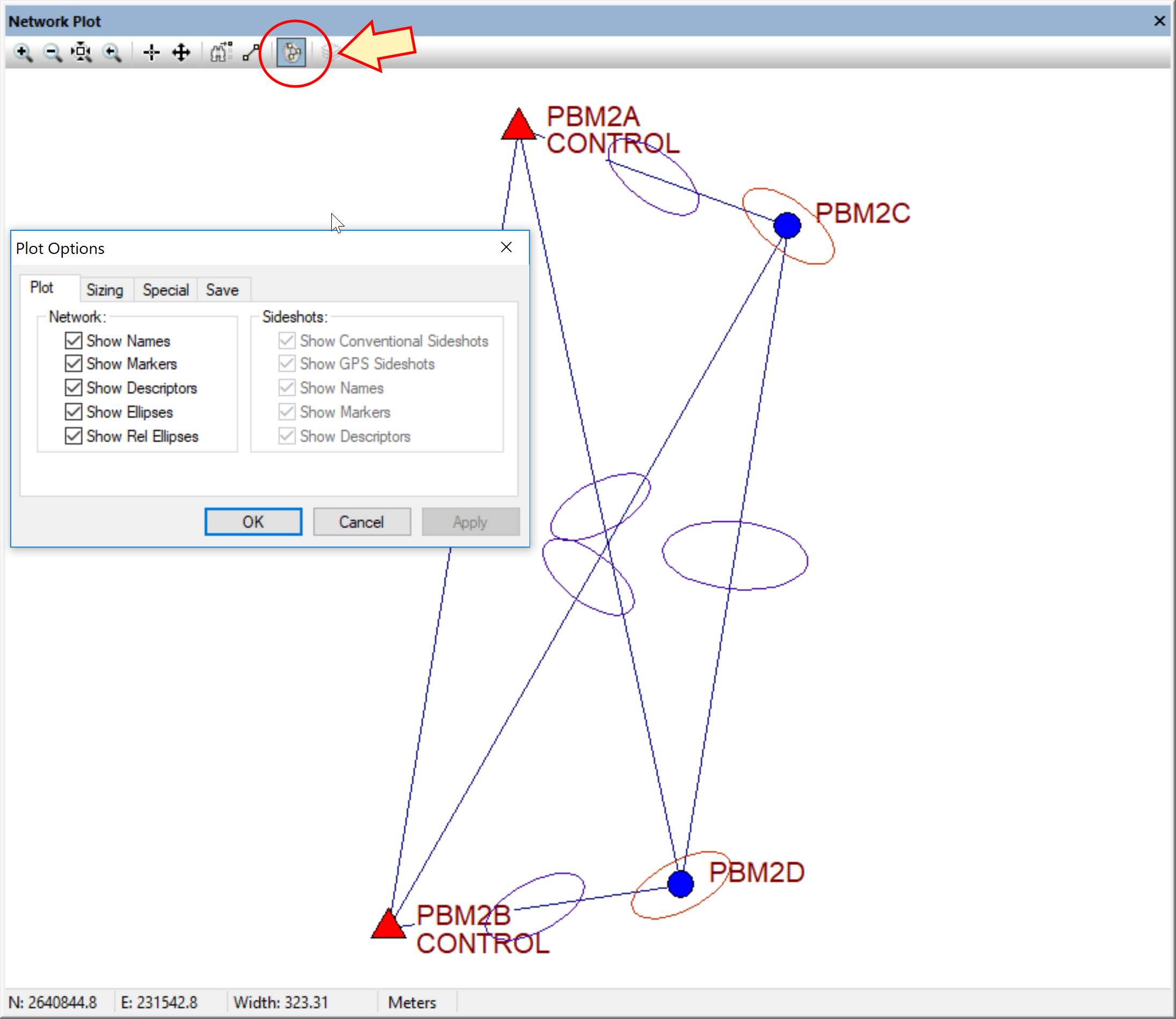 
ถ้าขนาดตัวหนังสือ ขนาดวงรีเล็กไปสามารถตั้งได้ที่แท็บ "Sizing" 
ในฐานะที่ผมเป็นผู้พัฒนาโปรแกรมคำนวณวงรอบ "Traverse Pro" แบบ single loop ถ้าเทียบความยากง่ายในการพัฒนาโปรแกรมกับ Star*Net แล้วเหมือนเม็ดทรายหนึ่งกำเมื่อเทียบกับทรายทั้งหาดทราย ผมชอบ Star*Net ตรงที่รูปแบบการป้อนข้อมูลถึงแม้จะป้อนแบบพิมพ์เข้าไปก็ตาม แต่ก็ออกแบบมาให้ง่ายทั้งรูปแบบข้อมูล มุม ระยะทาง ระดับ รายการคำนวณก็ละเอียดครบถ้วนสามารถปรินท์ส่งงานให้เจ้าของงานได้สบาย Network plot ก็ดูดี ถ้ามีความจำเป็นต้องใช้งานก็อุดหนุน ควักเงินซื้อลิขสิทธิ์ได้ครับ หรือมีหมุดไม่เกิน 10 หมุดหรือข้อมูลรังวัดจากสนามไม่เกิน 100 ข้อมูล สามารถใช้งานได้ฟรีเต็มฟีเจอร์